| Fundamental dynamics of collisionless magnetized plasma |
 |
| Kinetic modeling of sheared plasma flows |
 |
| Two-dimensional model of a sheared flow layer |
 |
 |
|
Two-dimensional model of a sheared flow layer
|
 |
|
Sestero's one-dimensional model (1966) of a tangential discontinuity (TD) with plasma velocity sheared in the direction perpendicular to the magnetic field lines has been extended to take into account a gradient of velocity (or shear) parallel to the magnetic field lines. Starting from previous kinetic 1D models of TDs (Lemaire and Burlaga, 1976; Roth et al., 1996) we have developed a two dimensional, steady-state solution of a boundary layer (BL) at the interface between two plasma flows. Inside the BL we consider a gradient of the electric and magnetic field, E(y,z) and B(y,z), and plasma variables, Vx(y,z) and n(y,z), in the direction parallel to the magnetic field direction. The velocity distribution function of each plasma species (electrons and protons) has been written as a function of two constants of motion, total energy and the canonical memntum corresponding to the ignorable coordinate. A third constant of motion, needed to determine the moments of the VDF, has been approximated by the magnetic moment, an adiabatic invariant. This approximation imposes certain constraints on the stationary model, as discussed by Echim (2004) and Echim and Lemaire (2005).
|
 |
|
The transition between a fast plasma jet and a background stagnant plasma takes place within a 2D boundary layer. The plasma bulk velocity is nearly uniform in the center of the jet; its value, Vx, is slightly different from the MHD convection velocity, UE = ExB. A novel feature, not present in previous 1D model of TD is the nonvanishing parallel (or magnetic field aligned) component of the electric field. The parallel E-fields are localized inside the boundary layer; they are almost equal to zero near the center of the jet as well as in the background stagnant plasma. The magnitude of the parallel electric field is anti-correlated with the parallel gradient of the electron density and correlated with the parallel gradient of the plasma bulk velocity. It is this non-MHD parallel electric field that allows the plasma from different parts of the magnetic field tubes to drift with different convection velocities. The contribution of the parallel shear of the perpendicular velocity for producing a parallel electric field has been determined quantitatively for the first time by Echim (2004) and Echim and Lemaire (2005). Parallel electric fields localized inside the boundary layers of propagating plasmoids have been testified by recent laboratory experiments (Hurtig et al., 2003)
|

|
|
Two-dimensional contout plot of the lines of equal plasma speed (in red).
Black arrows are proportional to the local value of the magnetic fied; they also indicate its orientation (from Echim, 2004).
|
|
|
|
|
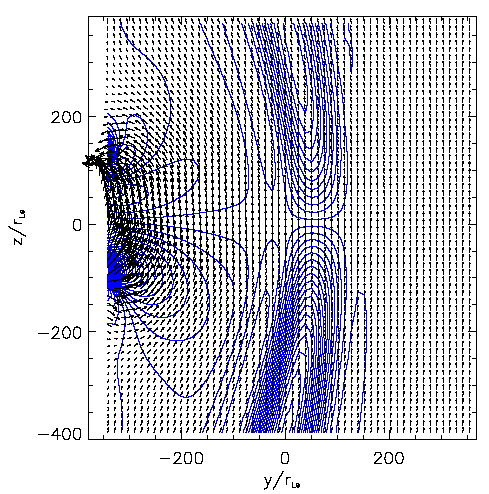
Two-dimensional contour plot of the parallel component of the electric field (in blue).
Arrows illustrate the local orientation and intensity of the magnetic field (from Echim, 2004).
|
|
|
|
 |
 |
References:
Echim, Ph. D. Thesis, Universite Chatolique de Louvain, 2004
Echim, M., J. Lemaire, Physical Review E, vol. 72, 036405, 2005
Hurtig, T., Brenning, N., Raadu, M.A., Physics of Plasmas, 10(11), 4291, 2003
Lemaire, J., and L.F. Burlaga, Astrophys. Space Sci., 45, 303, 1976
Sestero, A., Phys. Fluids, 9, 2006, 1966
Roth, M., J. De Keyzer, and M. Kuznetsova, Space Sci. Rev., 76, 251, 1996
|
 |
|
Contact: Dr. Marius Mihai Echim
|
