| Fundamental dynamics of collisionless magnetized plasma |
 |
| Kinetic modeling of sheared plasma flows |
 |
| Two-dimensional model of a sheared flow layer |
 |
 |
|
Kinetic modeling of sheared plasma flows
|
 |
|
The problem of the dynamics of a one-dimensional plasma slab moving across a magnetic field and a background plasma is treated in the framework of the kinetic theory. A velocity distribution function (VDF) is found for each plasma species, electrons and protons, in terms of the constants of motion defined by the geometry of the problem, total energy and canonical momentum. The zero and first order moments of the VDF are introduced into the right hand side term of Maxwell's equations to compute the electric and magnetic vector potentials and corresponding fields. The solutions are found numerically. We obtain a region of plasma convection - the slab proper - where the plasma moves with a uniform velocity, approximately equal to the MHD convection velocity. At the core's margins two plasma 'wings' form, each being the result of a pair of interpenetrated boundary layers with different transition lengths (Echim et al., 2005). Inside these wings, the plasma velocity is not uniform. It decreases from the maximum value obtained in the core to a minimum value in central region of the wings where a flow reversal is found with the plasma convecting in the opposite direction to the core motion. There is also an asymmetry of the velocity gradient at the borders of the core which results in a corresponding asymmetry in the thickness of the wings. Furthermore it is found that the reversed plasma flow in the thinner wing is larger than that in the broader wing. For a fixed direction of the magnetic field the two plasma wings interchange position with respect to the center of the slab when the plasma bulk velocity reverses sign.
|
 |
|
The width of the central core depends on the input parameters, mainly on the temperatures of the stagnant species and the bulk speed. Our results show that, like in hydrodynamical piston flows, the forward motion of a plasma element (a slab in this case) drives the backward motion of the adjacent layers. The distributions of plasma and fields are not the same at the two margins. When the sign of the core's velocity is changed but the direction of the external magnetic field is kept the same, the two asymmetric boundary layers and their interpenetrated current sheets interchange position. Our kinetic model demonstrates that the distributions of the plasma density, bulk velocity and electromagnetic fields inside a moving slab depend on the sign of the velocity with respect to the external magnetic field. Similar results were already found by Sestero (1966), Roth et al. (1996) and De Keyser and Roth (1998) in their 1D kinetic models of tangential discontinuities.
|
|
Spatial gradients of high-speed flows directed Earthward in the midtail plasma sheet have recently been determined by Nakamura et al. (2004) using multipoint measurements from the Cluster spacecraft. It was observed that the velocity gradient at the duskward edge of a flow tends to be sharper than that at the dawnward edge. This observations seem to confirm the predictions of our kinetic model.
|
|
 |
|
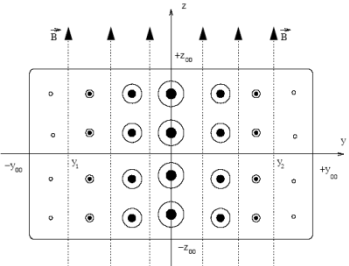
Diagram of the distribution of the plasma bulk velocity (circles whose radius is proportional to the local speed) and B-field for a 1D slab moving across magnetic field lines.
|
|
|
|
|
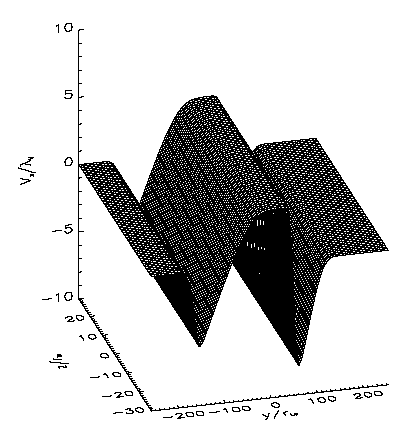
Solution for the plasma bulk velocity obtained as 1st order moment of the VDF. Note the asymmetry between left hand side and right hand side boundary layers.
|
|
|
|
 |

|
|
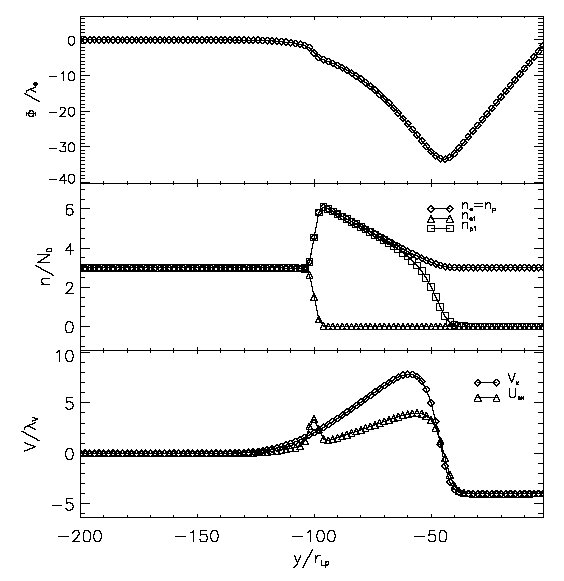
Cross section through the left hand side boundary layer of a 1D plasma slab moving with a positive velocity. Panels show the electric potential, the number density and bulk velocity.
|
|
|
|
|
Cross section through the left hand side boundary layer of a 1D plasma slab moving with a negative velocity. Same panel format as in the left figure. Note the asymmetry between the two figures.
|
|
|
|
 |
References:
Echim, M., Lemaire, J., Roth, M., Physics of Plasmas, vol. 12, 072904, 2005
De Keyser J. and M. Roth, J. Geophys. Res., 103, 6663, 1998
R. Nakamura, W. Baumjohann, C. Mouilis et al., Geophys. Res. Lett., 31, L09804, 2004
Roth, M., J. De Keyzer, and M. Kuznetsova, Space Sci. Rev., 76, 251, 1996
|
 |
|
Contact: Dr. Marius Mihai Echim
|
